Spherical Coordinate System

Previously, i was stuck with a very simple geometry question.  My question was simple "How do you take an existing point and map that to a 3D space?"  Why did i have such question?  I have a set of images with annotations.  Now i want to visualize them in 3D.  Note that the set of images were ordered radially.   Hopefully, below illustration would give the reader a better idea.



The dotted red circle and dotted purple circle are there to give a stronger scent of a 3D space and the arrangement of the 2D images(like a fan). It also indicates that each slice is about 1^o apart and a legend that'd give you an idea where the z-axis should be.

For peeps who are good at math would immediately recognize what i am trying to do and see the solution.  For a slow learner like me, it took me a while to flash back to basic geometry.

The solution is indeed very simple: Spherical Coordinate System.

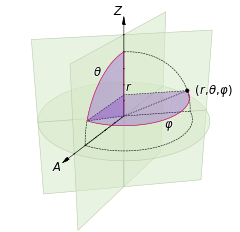Since, formally speaking, what i am trying to do is to convert spherical coordinates to Cartesian coordinates.  The correspoding (x,y,z) can then be expressed by:




I should have known better!